The Challenge Is on: Multi-Way Number Partitioning with T-SQL and SQL CLR
The challenge is known as multi-way number partitioning. Given a set of numbers S, representing quantities or weights, and a number of desired partitions, k, divide the quantities into k partitions such that the quantities are as evenly distributed among the partitions as possible.
February 21, 2018
Kola Tchernitsky of Zopa is a long-time SQL acquaintance of mine. His company has a great team of database pros, who appreciate programming challenges. Kola gave me one of his programming challenges to see how I’d approach it in SQL Server. In this article I describe the challenge and provide both T-SQL-based and CLR-based solutions. Thanks, Kola, for the lovely puzzle!
I’d also like to thank Adam Machanic, Tobias Ternstrom and Davide Mauri for the discussions we had on the CLR-based solutions, and for the advice they offered.
The Challenge and the Chosen Algorithm
The challenge is known as multi-way number partitioning. Given a set of numbers S, representing quantities or weights, and a number of desired partitions, k, divide the quantities into k partitions such that the quantities are as evenly distributed among the partitions as possible. For Kola, the number of partitions was two, but I’ll describe solutions both for k = 2 and for k >= 2. Also, Kola didn’t require the distribution to be completely optimal--rather, he was happy with a solution that produces a close-enough-to-optimal distribution, as long as it performed well.
This problem is in the same family of problems as bin packing. Solutions that guarantee optimal distribution are quite expensive and don’t scale well. However, if you can compromise a bit on the optimality of the distribution, you can use a greedy heuristic known as the first-fit decreasing algorithm, which has O(n log n) complexity—much better than the alternatives.
The algorithm is simple:
· Scan the items in descending quantity order
· For each item, assign the quantity to the group with the lowest total quantity, or to the first group if they all have the same total quantity
According to this Wikipedia article, with k = 2, this greedy algorithm provides a 7/6-approximation to the optimal distribution. That is, the maximum total quantity among the groups produced by the greedy algorithm is less than or equal to 7/6ths of the maximum total quantity among the groups in an optimal distribution.
For example, given the set S = {7, 5, 6, 4, 8} and k = 2, the greedy algorithm produces the sets A = {4, 5, 8}, B = {6, 7}. An optimal distribution is A = {4, 5, 6}, B = {7, 8}. The maximum of the sums in the greedy approach is 17 and in the optimal case 15. Indeed, 17 <= 15 * 7/6 (=17.5).
I have looked for good performing noniterative solutions that implement the greedy approach in T-SQL, but haven’t found one yet. So, in this article I’ll focus on iterative solutions, using both T-SQL and SQL CLR.
Sample Data and Expected Results
I’ll use a database called mwaypart to hold the sample data for this article. Run the following code to create the database if it doesn’t already exist:
SET NOCOUNT ON;IF DB_ID(N'mwaypart') IS NULL CREATE DATABASE mwaypart;GOUSE mwaypart;Use the following code to create a table called T1, with a column called ID as the key, and a column called qty as the quantity, and populate it with a small set of sample data to check the validity of your solutions:
DROP TABLE IF EXISTS dbo.T1;GO CREATE TABLE dbo.T1( id INT NOT NULL CONSTRAINT PK_T1 PRIMARY KEY, qty INT NOT NULL); CREATE UNIQUE INDEX idx_qtyD_idD ON dbo.T1(qty DESC, id DESC); INSERT INTO dbo.T1(id, qty) VALUES (1, 6), (2, 4), (3, 8), (4, 5), (5, 7);Notice the index on the columns qty DESC, id DESC. The index holds the quantities in the order that you are supposed to process them using the greedy algorithm—first by quantity, descending, then by ID, descending as a tiebreaker.
Here’s the expected result for two-way partitioning:
id qty grp----------- ----------- -----------3 8 15 7 21 6 24 5 12 4 1
Here’s the expected result for three-way partitioning:
id qty grp----------- ----------- -----------3 8 15 7 21 6 34 5 32 4 2
To test the performance of your solutions, you will need a large set of sample data. First, run the following code to create the dbo.GetNums helper function:
CREATE OR ALTER FUNCTION dbo.GetNums(@low AS BIGINT, @high AS BIGINT) RETURNS TABLEASRETURN WITH L0 AS (SELECT c FROM (SELECT 1 UNION ALL SELECT 1) AS D(c)), L1 AS (SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B), L2 AS (SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B), L3 AS (SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B), L4 AS (SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B), L5 AS (SELECT 1 AS c FROM L4 AS A CROSS JOIN L4 AS B), Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum FROM L5) SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n FROM Nums ORDER BY rownum;GO
Next, run the following code to populate T1 with 1,000,000 rows:
DROP TABLE IF EXISTS dbo.T1;GO DECLARE @numrows AS BIGINT = 1000000, @maxqty AS INT = 1000; CREATE TABLE dbo.T1( id INT NOT NULL, qty INT NOT NULL); INSERT INTO dbo.T1 WITH (TABLOCK) (id, qty) SELECT n, ABS(CHECKSUM(NEWID())) % @maxqty + 1 AS qty FROM dbo.GetNums(1, @numrows); ALTER TABLE dbo.T1 ADD CONSTRAINT PK_T1 PRIMARY KEY(id);CREATE UNIQUE INDEX idx_qtyD_idD ON dbo.T1(qty DESC, id DESC);
Some of the solutions that I’ll cover in this article use memory-optimized table variables. Run the following code to enable In-Memory OLTP in the database. (This code assumes that you have a folder called C:mwaypart in your filesystem.):
ALTER DATABASE mwaypart ADD FILEGROUP mwaypart_MO CONTAINS MEMORY_OPTIMIZED_DATA; ALTER DATABASE mwaypart ADD FILE ( NAME = mwaypart_dir, FILENAME = 'C:mwaypartmwaypart_dir' ) TO FILEGROUP mwaypart_MO;
Two-way Partitioning with a Cursor-Based Solution
The following code implements a solution to two-way partitioning using the greedy algorithm with a T-SQL cursor and a disk-based table variable:
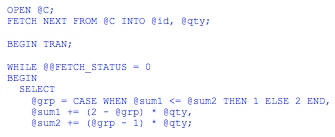
SET NOCOUNT ON; DECLARE @Result AS TABLE( id INT NOT NULL, qty INT NOT NULL, grp INT NOT NULL, INDEX idx_qtyD_idD UNIQUE CLUSTERED(qty DESC, id DESC)); DECLARE @id AS INT, @qty AS INT, @grp AS INT, @sum1 AS INT = 0, @sum2 AS INT = 0, @C AS cursor; SET @C = CURSOR FORWARD_ONLY STATIC READ_ONLY FOR SELECT id, qty FROM dbo.T1 ORDER BY qty DESC, id DESC; OPEN @C;FETCH NEXT FROM @C INTO @id, @qty; BEGIN TRAN; WHILE @@FETCH_STATUS = 0BEGIN SELECT @grp = CASE WHEN @sum1 <= @sum2 THEN 1 ELSE 2 END, @sum1 += (2 - @grp) * @qty, @sum2 += (@grp - 1) * @qty; INSERT INTO @Result(id, qty, grp) VALUES(@id, @qty, @grp); FETCH NEXT FROM @C INTO @id, @qty;END; COMMIT TRAN; SELECT id, qty, grp FROM @Result;
The code uses a cursor variable, so there’s no need to close and deallocate it explicitly; rather, the closing and deallocating happens automatically when the batch terminates. The code fetches the rows from the cursor one at a time into local variables in the order of qty, descending, id, descending. In each iteration, @sum1 holds the current total quantity for group 1 and @sum2 for group 2. The variable @grp is set to 1 if @sum1 is less than or equal to @sum2, and 2 otherwise. If @grp is 1, the current quantity is added to @sum1, otherwise to @sum2. This is done mathematically with the following assignments:
SELECT @grp = CASE WHEN @sum1 <= @sum2 THEN 1 ELSE 2 END, @sum1 += (2 - @grp) * @qty, @sum2 += (@grp - 1) * @qty;
The expression 2 - @grp is 1 when @grp is 1 and 0 when @grp is 2.
The expression @grp - 1 is 0 when @grp is 1 and 1 when @grp is 2.
If you find this logic confusing, you can replace it with the following:
SET @grp = CASE WHEN @sum1 <= @sum2 THEN 1 ELSE 2 END;
IF @grp = 1
SET @sum1 += @qty;
ELSE
SET @sum2 += @qty;
The code then inserts a row with the current ID, quantity and group into the table variable.
All insertions are done in a single transaction for efficiency.
Lastly, the code queries the table variable to return the final desired result.
This solution ran for 17 seconds on my system against the large set of sample data with the 1,000,000 rows.
One way to optimize the solution while still using T-SQL is to replace the disk-based table variable with a memory-optimized one. This will reduce I/O costs and remove the need for latching. To achieve this, you first need to create a memory-optimized table type, like so:
DROP TYPE IF EXISTS TYPE_mwaypart;GO CREATE TYPE dbo.TYPE_mwaypart AS TABLE( id INT NOT NULL, qty INT NOT NULL, grp INT NOT NULL,-- INDEX idx_qtyD_idD UNIQUE NONCLUSTERED(qty DESC, id DESC) INDEX idx_id NONCLUSTERED HASH (id) WITH (BUCKET_COUNT = 1048576))WITH (MEMORY_OPTIMIZED = ON);
Notice that the current code uses a hash index, but alternatively you can test a solution with a tree index instead (currently commented in the code). Here’s the modified solution, this time using a memory-optimized table variable based on the table type you just created:
SET NOCOUNT ON; DECLARE @Result AS TYPE_mwaypart; DECLARE @id AS INT, @qty AS INT, @grp AS INT, @sum1 AS INT = 0, @sum2 AS INT = 0, @C AS cursor; SET @C = CURSOR FORWARD_ONLY STATIC READ_ONLY FOR SELECT id, qty FROM dbo.T1 ORDER BY qty DESC, id DESC; OPEN @C;FETCH NEXT FROM @C INTO @id, @qty; BEGIN TRAN; WHILE @@FETCH_STATUS = 0BEGIN SELECT @grp = CASE WHEN @sum1 <= @sum2 THEN 1 ELSE 2 END, @sum1 += (2 - @grp) * @qty, @sum2 += (@grp - 1) * @qty; INSERT INTO @Result(id, qty, grp) VALUES(@id, @qty, @grp); FETCH NEXT FROM @C INTO @id, @qty;END; COMMIT TRAN; SELECT id, qty, grp FROM @Result;
This solution ran on my system for 12 seconds with a hash index and for 14 seconds with a tree index. There is an improvement compared to the first solution, but the improvement is not dramatic.
Multi-way Partitioning with a Cursor-based Solution
Handling k-way number partitioning, where k > 2, is not realistic with individual variables holding the intermediate group quantities. One option is to use a table variable holding per group the group number (column grp) and current group quantity (column sumqty). You want to index the table by (sumqty, grp) so that the top 1 row in index order will always have the group that the current quantity should be associated with. Here’s the code you should use to define this table variable (first, as a disk-based table):
DECLARE @Groups AS TABLE( grp INT NOT NULL, sumqty INT NOT NULL, INDEX idx_grp_sumqty UNIQUE CLUSTERED(sumqty, grp));
You initially populate the table variable with a zero quantity for all groups:
INSERT INTO @Groups(grp, sumqty) SELECT n AS grp, 0 AS sumqty FROM dbo.GetNums(1, @numgroups) AS Nums;
Then, in each round of the loop, you modify the top 1 row in (sumqty, grp) order, adding the current quantity to the sumqty value, and write a new row with the current id, qty and grp into the table variable @Result. Amazingly, this can be done in a single statement using a CTE and an UPDATE statement with an OUTPUT INTO clause, like so:
WITH C AS ( SELECT TOP (1) grp, sumqty FROM @Groups ORDER BY sumqty, grp ) UPDATE C SET sumqty += @qty OUTPUT @id, @qty, inserted.grp INTO @Result(id, qty, grp);
Here’s the complete solution code, with 10 as the number of groups:
SET NOCOUNT ON; DECLARE @Groups AS TABLE( grp INT NOT NULL, sumqty INT NOT NULL, INDEX idx_grp_sumqty UNIQUE CLUSTERED(sumqty, grp)); DECLARE @Result AS TABLE( id INT NOT NULL, qty INT NOT NULL, grp INT NOT NULL, INDEX idx_qtyD_idD UNIQUE CLUSTERED(qty DESC, id DESC)); DECLARE @id AS INT, @qty AS INT, @numgroups AS INT = 10, @C AS cursor; INSERT INTO @Groups(grp, sumqty) SELECT n AS grp, 0 AS sumqty FROM dbo.GetNums(1, @numgroups) AS Nums; SET @C = CURSOR FORWARD_ONLY STATIC READ_ONLY FOR SELECT id, qty FROM dbo.T1 ORDER BY qty DESC, id DESC; OPEN @C;FETCH NEXT FROM @C INTO @id, @qty; BEGIN TRAN; WHILE @@FETCH_STATUS = 0BEGIN WITH C AS ( SELECT TOP (1) grp, sumqty FROM @Groups ORDER BY sumqty, grp ) UPDATE C SET sumqty += @qty OUTPUT @id, @qty, inserted.grp INTO @Result(id, qty, grp); FETCH NEXT FROM @C INTO @id, @qty;END; COMMIT TRAN; SELECT id, qty, grp FROM @Result;
This solution took 31 seconds to complete on my system, specifying 10 as the number of groups, with the large set of sample data, using disk-based table variables.
To test the solution with memory-optimized table variables, you’ll also need a table type for the table variable @Groups. Here’s the code to create such a table type:
DROP TYPE IF EXISTS TYPE_mwaygroups;GO CREATE TYPE dbo.TYPE_mwaygroups AS TABLE( grp INT NOT NULL, sumqty INT NOT NULL, INDEX idx_grp_sumqty UNIQUE NONCLUSTERED(sumqty, grp))WITH (MEMORY_OPTIMIZED = ON);
Here’s the modified solution’s code replacing both disk-based table variables with memory optimized ones:
SET NOCOUNT ON; DECLARE @Groups AS TYPE_mwaygroups, @Result AS TYPE_mwaypart; DECLARE @id AS INT, @qty AS INT, @numgroups AS INT = 10, @C AS cursor; INSERT INTO @Groups(grp, sumqty) SELECT n AS grp, 0 AS sumqty FROM dbo.GetNums(1, @numgroups) AS Nums; SET @C = CURSOR FORWARD_ONLY STATIC READ_ONLY FOR SELECT id, qty FROM dbo.T1 ORDER BY qty DESC, id DESC; OPEN @C;FETCH NEXT FROM @C INTO @id, @qty; BEGIN TRAN; WHILE @@FETCH_STATUS = 0BEGIN WITH C AS ( SELECT TOP (1) grp, sumqty FROM @Groups ORDER BY sumqty, grp ) UPDATE C SET sumqty += @qty OUTPUT @id, @qty, inserted.grp INTO @Result(id, qty, grp); FETCH NEXT FROM @C INTO @id, @qty;END; COMMIT TRAN; SELECT id, qty, grp FROM @Result;
This code took 18 seconds to complete on my system.
As you can see, you do achieve improvements by using memory-optimized table variables, but they’re not really dramatic. There’s still a pretty high penalty associated with the fetching of the cursor records and the T-SQL iterations. If you want to see some dramatic improvements, you need to consider a CLR-based solution.
SQL CLR-based Solutions
I’ll present three CLR user-defined table-valued functions: a niladic function called PartitionTwoWays, which handles two-way number partitioning, and functions called PartitionMultipleWays and PartitionMultipleWays2, which accept a parameter called numgroups with the desired number of groups, and handle multi-way number partitioning using two different solutions.
Here’s the complete code defining a class called MultiWayPartitioning with all three functions (in your code, you should set the “data source” parameter to reflect your instance instead of “data source=.\sql2017”), followed by deployment instructions, and explanations:
using System;using System.Collections;using System.Collections.Generic;using System.Data;using System.Data.SqlClient;using System.Data.SqlTypes;using Microsoft.SqlServer.Server; public partial class MultiWayPartitioning{ private struct ResultRow { public SqlInt32 id; public SqlInt32 qty; public SqlInt32 grp; } public static void Partition_FillRow(Object obj, out SqlInt32 id, out SqlInt32 qty, out SqlInt32 grp) { ResultRow resultRow = (ResultRow)obj; id = resultRow.id; qty = resultRow.qty; grp = resultRow.grp; } [SqlFunction( DataAccess = DataAccessKind.Read, FillRowMethodName = "Partition_FillRow", TableDefinition = "id INT, qty INT, grp INT")] public static IEnumerable PartitionTwoWays() { using (SqlConnection conn = new SqlConnection("data source=.\sql2017;initial catalog=mwaypart;integrated security=SSPI;enlist=false")) { SqlCommand comm = new SqlCommand(); comm.Connection = conn; comm.CommandText = "SELECT id, qty FROM dbo.T1 ORDER BY qty DESC, id DESC;"; conn.Open(); SqlDataReader reader = comm.ExecuteReader(); ResultRow resultRow = new ResultRow(); SqlInt32 sum1 = 0; SqlInt32 sum2 = 0; while (reader.Read()) { resultRow.id = reader.GetSqlInt32(0); resultRow.qty = reader.GetSqlInt32(1); resultRow.grp = sum1 <= sum2 ? 1 : 2; sum1 += (2 - resultRow.grp) * resultRow.qty; sum2 += (resultRow.grp - 1) * resultRow.qty; yield return resultRow; } } } [SqlFunction( DataAccess = DataAccessKind.Read, FillRowMethodName = "Partition_FillRow", TableDefinition = "id INT, qty INT, grp INT")] public static IEnumerable PartitionMultipleWays(SqlInt32 numgroups) { SqlInt32[] groups = new SqlInt32[numgroups.Value]; for (int i = 0; i < numgroups; i++) groups[i] = 0; using (SqlConnection conn = new SqlConnection("data source=.\sql2017;initial catalog=mwaypart;integrated security=SSPI;enlist=false")) { SqlCommand comm = new SqlCommand(); comm.Connection = conn; comm.CommandText = "SELECT id, qty FROM dbo.T1 ORDER BY qty DESC, id DESC;"; conn.Open(); SqlDataReader reader = comm.ExecuteReader(); ResultRow resultRow = new ResultRow(); while (reader.Read()) { resultRow.id = reader.GetSqlInt32(0); resultRow.qty = reader.GetSqlInt32(1); resultRow.grp = 1; for (int i = 2; i <= numgroups; i++) if (groups[i - 1] < groups[resultRow.grp.Value - 1]) resultRow.grp = i; groups[resultRow.grp.Value - 1] += resultRow.qty; yield return resultRow; } } } [SqlFunction( DataAccess = DataAccessKind.Read, FillRowMethodName = "Partition_FillRow", TableDefinition = "id INT, qty INT, grp INT")] public static IEnumerable PartitionMultipleWays2(SqlInt32 numgroups) { SortedList sl = new SortedList(); for (int i = 1; i <= numgroups; i++) sl.Add((SqlDecimal)(i / 10000000000.0), (SqlInt32)i); using (SqlConnection conn = new SqlConnection("data source=.\sql2017;initial catalog=mwaypart;integrated security=SSPI;enlist=false")) { SqlCommand comm = new SqlCommand(); comm.Connection = conn; comm.CommandText = "SELECT id, qty FROM dbo.T1 ORDER BY qty DESC, id DESC;"; conn.Open(); SqlDataReader reader = comm.ExecuteReader(); ResultRow resultRow = new ResultRow(); while (reader.Read()) { resultRow.id = reader.GetSqlInt32(0); resultRow.qty = reader.GetSqlInt32(1); resultRow.grp = (SqlInt32)sl.GetByIndex(0); SqlDecimal key = (SqlDecimal)sl.GetKey(0); sl.RemoveAt(0); sl.Add((SqlDecimal)(key + resultRow.qty), resultRow.grp); yield return resultRow; } } }} Notice that in order to stream the result rows to the caller as they become available, the code uses the “yield return” construct. Due to a bug, you need to instruct SQL Server not to enlist the connection into the current transaction. This means that you cannot use SqlConnection("context connection=true"); rather, use a typical explicit client connection string, and include “enlist=false.” Your complete connection string should look like this: SqlConnection("data source=;initial catalog=;integrated security=SSPI;enlist=false"). This also means that the assembly needs to be created with a minimum permission set of EXTERNAL_ACCESS. Consequentially, the assembly needs to be trusted (signed with a certificate or an asymmetric key that has a corresponding login with the right permission, or new to SQL Server 2017, whitelisted using the sp_add_trusted_assembly procedure). Here, I’ll just enable the TRUSTWORTHY database option for simplicity.
After building the assembly into a .dll, here’s the code to deploy it and the three functions in the database mwaypart (replace the path to the .dll file as needed):
ALTER DATABASE mwaypart SET TRUSTWORTHY ON; DROP FUNCTION IF EXISTS dbo.PartitionTwoWays;DROP FUNCTION IF EXISTS dbo.PartitionMultipleWays;DROP FUNCTION IF EXISTS dbo.PartitionMultipleWays2;DROP ASSEMBLY IF EXISTS MultiWayPartitioning; CREATE ASSEMBLY MultiWayPartitioning FROM 'C:MultiWayPartitioningMultiWayPartitioningbinDebugMultiWayPartitioning.dll'WITH PERMISSION_SET = EXTERNAL_ACCESS;GO CREATE FUNCTION dbo.PartitionTwoWays() RETURNS TABLE(id INT, qty INT, grp INT)AS EXTERNAL NAME MultiWayPartitioning.MultiWayPartitioning.PartitionTwoWays;GO CREATE FUNCTION dbo.PartitionMultipleWays(@numgroups AS INT) RETURNS TABLE(id INT, qty INT, grp INT)AS EXTERNAL NAME MultiWayPartitioning.MultiWayPartitioning.PartitionMultipleWays;GO CREATE FUNCTION dbo.PartitionMultipleWays2(@numgroups AS INT) RETURNS TABLE(id INT, qty INT, grp INT)AS EXTERNAL NAME MultiWayPartitioning.MultiWayPartitioning.PartitionMultipleWays2;
A few words about the code defining the class and the functions. The class starts by defining a structure called ResultRow representing a result row, and a fill row method called Partition_FillRow to fill a result row. All three functions use this fill row method, and set the result table definition (TableDefinition attribute) to "id INT, qty INT, grp INT".
All three functions define a SqlConnection object called conn based on the aforementioned connection string, a SqlCommand object called comm based on the query "SELECT id, qty FROM dbo.T1 ORDER BY qty DESC, id DESC;" and a SqlDataReader object called reader to iterate through the command’s query result rows one at a time.
Other than the fact that the function PartitionTwoWays is written using .NET code, it implements the very same algorithm as the T-SQL solution for two-way number partitioning. Use the following code to test the function:
SELECT * FROM dbo.PartitionTwoWays();
Recall that the T-SQL solution ran for 18 seconds with a disk-based table variable, and 12 seconds with a memory optimized one against the large set of sample data on my system. The CLR-based function finished in 2 seconds!
As for multi-way number partitioning, the function PartitionMultipleWays defines a simple array to hold the current total quantity per group:
SqlInt32[] groups = new SqlInt32[numgroups.Value];
The function first populates the array with a row per group with a quantity 0, like so:
for (int i = 0; i < numgroups; i++) groups[i] = 0;
Then, for every source quantity, the function finds the group with the minimum total quantity by looping through the array elements, setting the current row’s group to the one with the lower quantity, and adds the current quantity to that group’s total, like so:
resultRow.grp = 1; for (int i = 2; i <= numgroups; i++) if (groups[i - 1] < groups[resultRow.grp.Value - 1]) resultRow.grp = i; groups[resultRow.grp.Value - 1] += resultRow.qty;
Use the following code to test the function with 10 groups:
SELECT * FROM dbo.PartitionMultipleWays(10);
This simplistic algorithm for finding the group with the minimum total quantity works well for a small number of groups, but doesn’t scale well for a large number of groups. I got the following run times for a table with 1,000,000 rows with different numbers of groups:
10 groups: 3 seconds100 groups: 5 seconds
1000 groups: 44 seconds
If you need to deal with a large number of groups, you will want to replace the simplistic loop against the array to find the minimum with a more optimal alternative.
The PartitionMultipleWays2 function achieves a more optimal handling of a large number of groups with a SortedList object. The list holds pairs of key (object) and value (object) items, sorted by the key. So, you can use it to hold the group states, with the group’s current total quantity as the key, and the group ID as the value. This way, the item at position 0 will always be the group with the minimum total quantity—the group that you should associate the next source quantity with. One tricky thing, though, is that the keys have to be unique, and obviously you could have states where multiple groups have the same total quantity. A possible solution is to store as the key a numeric value in the form: q.gggggggggg, where q is the current total quantity for the group, and gggggggggg is the group ID divided by 10000000000.0. For example, an item representing total quantity 180 for group 7 will be represented by the key 180.0000000007. This way, the key is guaranteed to be unique, and you even apply tiebreaking logic for multiple groups with the same total quantity, preferring the one with the lowest group ID.
The function first populates the list with an item per group, with the total quantity part of the key being 0 initially, like so:
SortedList sl = new SortedList(); for (int i = 1; i <= numgroups; i++) sl.Add((SqlDecimal)(i / 10000000000.0), (SqlInt32)i);
For every source quantity, the function sets the current row’s group ID to the one at position 0 in the list:
resultRow.grp = (SqlInt32)sl.GetByIndex(0);
Then the code is supposed to update the total quantity of the list item at position 0 by adding the source quantity, but a SortedList object doesn’t support updating the key; to solve this, you removre and add an item, like so:
SqlDecimal key = (SqlDecimal)sl.GetKey(0); sl.RemoveAt(0); sl.Add((SqlDecimal)(key + resultRow.qty), resultRow.grp);
et voilà!
Use to following code to test the function with 1,000 groups:
SELECT * FROM dbo.PartitionMultipleWays2(1000);
This code finished in 5 seconds on my system—not bad compared to the 44 seconds it took the PartitionMultipleWays function to process that many groups.
Summary
As much as I tried, alas, I couldn’t find a good performing noniterative solution to the multi-way number partitioning problem. It doesn’t mean that one doesn’t exist, though. I’ll keep looking for one, and you should, too! If you find something, be sure to let me know.
The cursor-based iterative T-SQL solutions don’t perform as well as the CLR-based solutions due to the high cost of the cursor fetching and iterations in T-SQL. As of SQL Server 2017, natively compiled modules don’t support cursors. If they ever do, it will be interesting to give the T-SQL solutions another whirl, since in natively compiled mode they are likely going to perform dramatically better.
About the Author(s)
You May Also Like
.jpg?width=700&auto=webp&quality=80&disable=upscale)


_(1).png?width=700&auto=webp&quality=80&disable=upscale)

.png?width=700&auto=webp&quality=80&disable=upscale)